Conditional Expectation Random Variable

If the conditional distribution of Y displaystyle Y given X displaystyle X is a continuous distribution then its probability density function is known as the conditional density function. 0 pi 1.

How To Find The Expected Value Of Two Dependent Random Variables E X Z Quora

Distributions of Functions of Random Variables.

. Conditional probability is the probability of one thing being true given that another thing is true and is the key concept in Bayes. 201 - Two Continuous Random Variables. Begingroup If youre looking for direct answers to this particular question note that routine book-work style questions such as this should carry the self-study tag and you should read its tag-wiki and modify your question to follow the guidelines on asking such questions - youll need to clearly identify what youve done to solve the problem yourself and indicate the specific help.

We have used di erent fonts for the Eof conditional expectation and the E of usual expectation in order to emphasize that the conditional. So it is a function of y. De nition The conditional expectation EY jF n is the unique random variable satisfying the following.

The conditional distribution contrasts with the marginal distribution of a random variable which is its distribution without reference to the value of the other variable. This is distinct from joint probability which is the probability that both things are true without knowing that one of them must be true. If we consider EXjY y it is a number that depends on y.

EY jF n is F n-measurable. We will also discuss conditional variance. 211 - Conditional Distribution of Y Given X.

212 - Joint PDF. Individual conditional expectation ICE plot Similar to a PDP an individual conditional expectation ICE plot shows the dependence between the target function and an input feature of interest. A2 Conditional expectation as a Random Variable Conditional expectations such as EXjY 2 or EXjY 5 are numbers.

Px is the probability density function. Discrete Random Variable. 211 - Conditional Distribution of Y Given X.

The one problem for generating data with VAE is we do not have any control over what kind of data it generates. Expectation of discrete random variable. The examples given.

Functions of One Random Variable. Theorem 1 Expectation Let X. Pi 1 where sum is taken over all possible values of x.

202 - Conditional Distributions for Continuous Random Variables. The mathematical expectation is denoted by the formula. 201 - Two Continuous Random Variables.

Expectation of continuous random variable. Calculating expectations for continuous and discrete random variables. In particular the following theorem shows that expectation preserves the inequality and is a linear operator.

Let E denote the mathematical expectation operator ie the population average of a random variable. EX Σ x 1 p 1 x 2 p 2 x n p n where x is a random variable with the probability function fx. The formula for the conditional mean of given involves an integral which can be thought of as the limiting case of the summation found in the discrete case above.

Where Fx is the distribution function of X. Of X and Y. A dummy variable Di.

For every F n-measurable event A EEY jF n1 A EY1 A. An important concept here is that we interpret the conditional expectation as a random variable. For a random variable expected value is a useful property.

The probability function associated with it is said to be PMF Probability mass function. If we train it well the images will be good but we will have no. For a continuous random variable the expectation is sometimes written as EgX Z x gx dFx.

212 - Joint PDF. The proposition in probability theory known as the law of total expectation the law of iterated expectations LIE Adams law the tower rule and the smoothing theorem among other names states that if is a random variable whose expected value is defined and is any random variable on the same probability space then ie the expected value of the conditional. The expectation of a random variable X condi-tional on the value taken by another random variable Y.

EX is the expected value and can be computed by the summation of the overall distinct values that is the random variable. For each individual we observe Yi Y0i DiY1i Y0i that is we observe Y1i for trainees and Y0i for everyone else. In probability and statistics the expectation or expected value is the weighted average value of a random variable.

If the value of Y affects the value of X ie. However unlike a PDP which shows the average effect of the input feature an ICE plot visualizes the dependence of the prediction on a feature for each sample separately with one. Functions of One Random Variable.

Of X and Y. For example if we train a VAE with the MNIST data set and try to generate images by feeding Z N01 into the decoder it will also produce different random digits. In Section 513 we briefly discussed conditional expectation.

A random variable X is said to be discrete if it takes on finite number of values. Pxi Probability that X xi PMF of X pi. X and Y are dependent the conditional expectation of X given the value of Y will be different from the overall expectation.

Conditional expectation of a continuous random variable Let us now tackle the case in which and are continuous random variables forming a continuous random vector. Here we will discuss the properties of conditional expectation in more detail as they are quite useful in practice. In this section we will study a new object EXjY that is a random variable.

We start with an example. X is the value of the continuous random variable X. The expectation operator has inherits its properties from those of summation and integral.

EX is the expectation value of the continuous random variable X. Roll a die until we get a 6. For continuous random variables EYi yfydy where fy is the density of Yi.

For example one joint probability is the probability that your left and right socks are both black. 2 Conditional Probability and Independence5 3 Discrete Random Variables7 4 Continuous Random Variables10 5 The Normal Distribution13 6 Expectation and Variance17 7 Joint Distributions and Independence19 8 Covariance and Correlation22 9 Random Vectors24 10 Transformations of Random Variables26 11 The Law of Large Numbers29 12 Moment. 202 - Conditional Distributions for Continuous Random Variables.

Distributions of Functions of Random Variables.

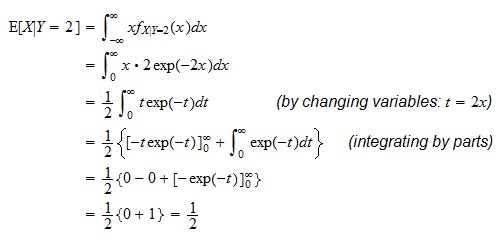
Conditional Expectation Definition Formula Examples

L13 2 Conditional Expectation As A Random Variable Youtube

Conditional Expectation Of A Function Of A Random Variable Youtube

L13 2 Conditional Expectation As A Random Variable Youtube